Swift는 RandomAccessCollection 타입에 대해서 기본 sort() 메소드를 제공합니다. 이 sort()메소드는 TimSort라는 정렬 알고리즘을 사용합니다. 이번 포스트에서는 이 TimSort와, 이 Timsort의 기반이 되는 InsertionSort와 MergeSort에 대해서도 알아보겠습니다.
-
Insertion Sort
Insertion Sort는 배열의 일부를 정렬된 상태로 유지하면서, 다음 원소가 있어야 할 위치를 정렬된 부분에서 찾아서 해당 위치에 원소를 삽입하는 정렬방식입니다.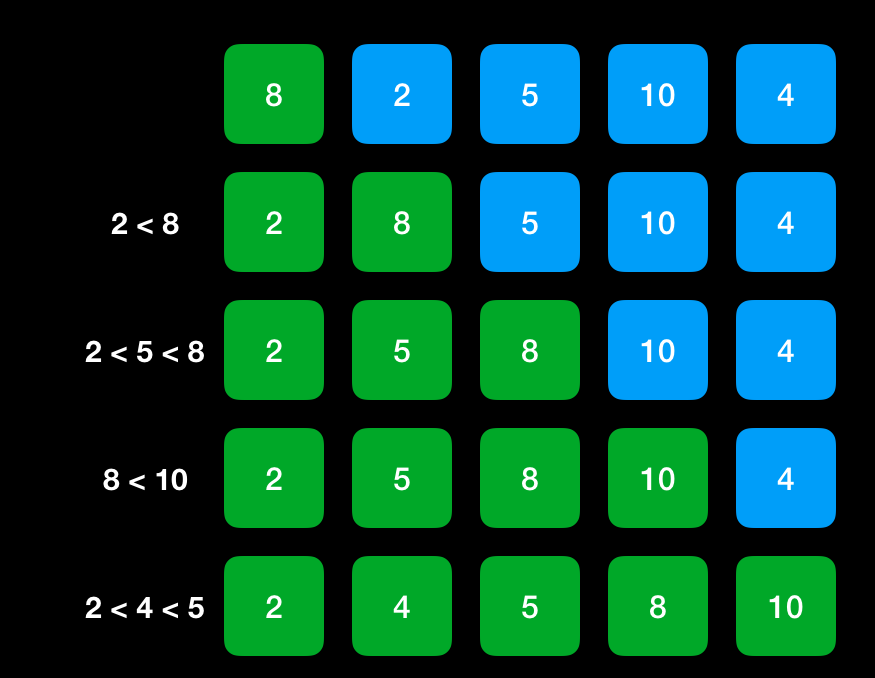
extension Array { mutating func insertionSort(by comparer: (Element, Element) -> Bool) { insertionSort(0, count, by: comparer) } private mutating func insertionSort(_ begin:Int, _ end: Int, by comparer: (Element, Element) -> Bool) { for i in begin..<end { for j in stride(from: i, to: 0, by: -1) { if !comparer(self[j],self[j-1]) { break } self.swapAt(j, j-1) } } } }이 정렬 방식은 원소가 모두 정렬되어 있을 경우, 단순히 배열을 한번 훑기만 하므로 O(n)의 시간 복잡도를 가집니다. 최악의 경우는 원소가 거꾸로 정렬되어 있는 경우로, O(n^2)의 시간 복잡도를 가집니다. Insertion Sort는 또한 Stable Sort에 해당합니다.
-
Merge Sort
Merge Sort는 주어진 배열을 작은 크기로 쪼개서 정렬한 뒤에, 이를 순차적으로 합치는 정렬 방법입니다. 분할하는 방법에는 여러 방법이 있지만, 주로 절반씩 쪼개서 합치는 분할 정복 기법을 사용합니다.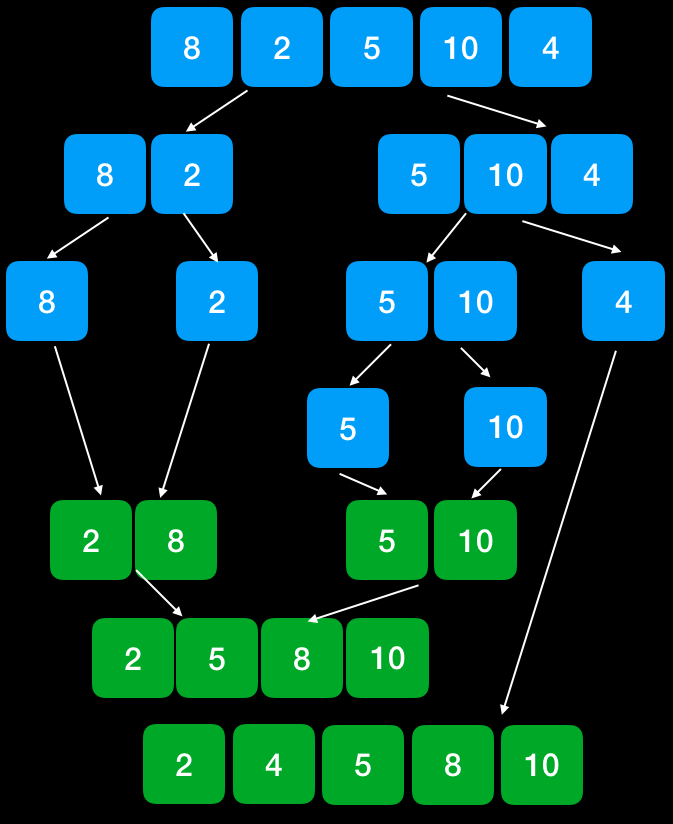
extension Array { mutating func mergeSort(by comparer: (Element, Element) -> Bool) { _mergeSort(0, count, by: comparer) } private mutating func _mergeSort(_ start: Int, _ end:Int, by comparer: (Element, Element) -> Bool) { let range = end - start if range < 2 { return } let mid = (start + end) / 2 _mergeSort(start, mid, by: comparer) _mergeSort(mid, end, by: comparer) merge(start, end, by:comparer) } private mutating func merge(_ start:Int, _ end: Int, by comparer: (Element, Element) -> Bool ){ self.insertionSort(start, end, by: comparer) } }Merge Sort는 분할을 할 때 마다 문제 크기가 절반으로 줄어듭니다. 대신 문제의 개수는 2배로 늘어납니다. 이 부분 문제는 O(1)로 정렬할 수 있을 때 까지(즉, 원소가 1개일 때까지) 수행되며, 이후 부분 문제들은 O(n)의 시간 복잡도를 가지는 알고리즘으로 합쳐집니다. 이 합쳐지는 과정은 문제의 개수에 비례해서 이루어지므로 전체 시간 복잡도는 O(n log n)이 됩니다. Merge Sort 역시 Stable Sort에 해당합니다.
원래 MergeSort의 Merge는 O(n)의 추가 공간을 사용하여 O(n)의 시간 복잡도를 달성합니다. 하지만 여기서는 이미 구현된 소트 방식을 활용하고 추가 공간을 사용하지 않기 위해 Merge과정을 InsertionSort로 대체하였습니다. 이 경우 평균 시간 복잡도가 O(n^2 log n)이지만 merge를 하는 배열은 정렬되어 있는 배열이기 때문에 정렬된 상태에서 좋은 성능을 발휘하는 Insertion Sort에서는 아주 나쁘지많은 않으리라 기대할 수 있습니다.
-
TimSort
드디어 TimSort를 알아 볼 차례입니다. Timsort는 Insertion Sort와 Merge Sort를 합친 하이브리드 소팅에 해당합니다. Timsort는 Run이라는 단위로 배열을 분할하고 이 분할된 단위에 대해 Insertion Sort를 수행한 뒤, 이를 합쳐서 정렬을 수행합니다. Timsort는 다음과 같은 과정을 통해 이루어집니다.-
minRun 상수 구하기: 가장 먼저, 배열을 분할할 크기 단위를 정하는 과정을 수행합니다. 이를 minRun이라고 하며, 이 값은 배열의 크기 값에 따라 유동적으로 정해집니다. Swift에서는 크기 64 이하의 배열에서는 배열의 크기로, 그 이상에 대해서는 비트의 배열에 따라서 32~64 사이의 값을 가지게 됩니다. 다음은 실제 Swift의 구현입니다(19/11/22 버전 기준)
internal func _minimumMergeRunLength(_ c: Int) -> Int { // Max out at `2^6 == 64` elements let bitsToUse = 6 if c < 1 << bitsToUse { return c } let offset = (Int.bitWidth - bitsToUse) - c.leadingZeroBitCount let mask = (1 << offset) - 1 return c >> offset + (c & mask == 0 ? 0 : 1) } -
run 만들기: 이후 non-descending(뒷 원소가 앞 원소보다 크거나 같다) 혹은 strictly descending(뒷 원소가 앞 원소보다 작다) 조건을 만족하는 크기로 배열을 분할합니다. 이후 strictly descending한 경우, 배열을 뒤집는 과정을 거칩니다. 이 때 분할한 배열의 크기가 minRun보다 작은 경우에는 minRun 크기가 되도록 배열을 확장한 뒤, Insertion Sort로 정렬합니다. 이는 최대한 적은 횟수로 머지를 수행하기 위해서는 조각의 크기가 균일해야 하기 때문입니다. 이렇게 만들어진 부분 배열을 Run이라고 하며, 이후 이를 스택에 넣습니다. 실제 구현에서는 배열을 직접 자르는 게 아니라 범위로 나타납니다.
-
Merge 혹은 다음 Run 구하기: 스택에 Run이 쌓였을 때, 이를 바로 Merge할 지 말지를 결정해야 합니다. swift의 TimSort에서는 다음과 같은 전략을 취합니다.
- 스택의 위에서부터 4개의 Run을 차례대로 X,Y,Z,W라고 하면, 다음 불변식을 만족해야 합니다.
- 스택 크기가 4이상 일 경우, |W| > |Z| + |Y|
- 스택 크기가 3일 경우, |Z| > |X| + |Y|
- 스택 크기가 2인 경우, |Y| > |X|
- 만약 조건을 만족하지 않는다면 Y를 X와 Z 중 작은 쪽과 합친다.
- 불변식을 만족하거나 스택 크기가 1이 되면 Merge를 종료하고 다음 Run을 구한다.
- 배열의 끝에 다다를 경우, 스택에 쌓여있던 모든 Run을 위에서부터 합쳐서 하나로 만듭니다.
다음은 그 구현입니다. 위에서 구현했던 Insertion Sort와 MergeSort를 이용하고 있습니다.
extension Array where Element == Range<Int> { // RunStack에서 이용하는 메소드 mutating func mergeRuns(_ merging: (Range<Int>) -> Void) { while count > 1 { var lastIndex = count - 1 if lastIndex >= 3, self[lastIndex - 3].count <= self[lastIndex-2].count + self[lastIndex-1].count { if self[lastIndex - 2].count < self[lastIndex].count { lastIndex -= 1 } } else if lastIndex >= 2, self[lastIndex - 2].count <= self[lastIndex - 1].count + self[lastIndex].count { if self[lastIndex - 2].count < self[lastIndex].count { lastIndex -= 1 } } else if self[lastIndex - 1].count <= self[lastIndex].count { // 바로 머지한다 } else { break } let mergedX = self.remove(at: lastIndex) let mergedY = self.remove(at: lastIndex-1) let merged = mergedY.lowerBound..<mergedX.upperBound merging(merged) self.insert(merged, at: lastIndex-1) } } private mutating func mergeAll(_ merging: (Range<Int>) -> Void) { while count > 1 { let mergedX = self.removeLast() let mergedY = self.removeLast() let merged = mergedY.lowerBound..<mergedX.upperBound merging(merged) self.append(merged) } } } extension Array { // TimSort 본체에서 이용하는 메소드와 프로퍼티들 private var minRun: Int { let bitsToUse = 6 if count < 1 << bitsToUse { return count } let offset = (Int.bitWidth - bitsToUse) - count.leadingZeroBitCount let mask = (1 << offset) - 1 return count >> offset + (count & mask == 0 ? 0 : 1) } private func getRun(_ start: Int, by comparer: (Element, Element) -> Bool) -> (Bool, Int){ guard start < count - 1 else { return (true, count) } let isDescending = comparer(self[start+1], self[start]) var previous = start var current = start + 1 repeat { previous = current current += 1 } while current < count && isDescending == comparer(self[current],self[previous]) return (isDescending, current) } private mutating func reverse(_ start: Int, _ end: Int) { var start = start var end = end while start < end { swapAt(start, end) start += 1 end -= 1 } } mutating func timSort(by comparer: (Element, Element) -> Bool) { if count <= minRun { insertionSort(by: comparer) } else { timSort(0, count, by: comparer) } } private mutating func timSort(_ start: Int, _ end: Int, by comparer: (Element, Element) -> Bool) { let minRun = self.minRun var runStack: [Range<Int>] = [] var start = startIndex while start < endIndex { var (isDescending, end) = getRun(start, by: comparer) if isDescending { reverse(start, end) } if end < endIndex, end - start < minRun { let newEnd = Swift.min(endIndex, start+minRun) insertionSort(start, newEnd, by: comparer) end = newEnd } runStack.append(start..<end) runStack.mergeRuns { merge($0.lowerBound, $0.upperBound, by: comparer) } start = end } runStack.mergeAll { merge($0.lowerBound, $0.upperBound, by: comparer) } } }TimSort는 현실 세계에서 사용하는 배열들이 완전 무작위가 아니라는 점에서 착안하여 정렬을 최적화한 좋은 예시로 최선의 때에는 O(n), 최악의 경우에도 O(n log n )의 시간 복잡도를 가집니다.
-
TimSort에 대해서 알아보았습니다. 여기서 Insertion Sort을 최적화한 Binary Insertion Sort 등을 적용한다던가로 내부 구현을 더 최적화하면 더 좋은 결과를 얻을 수 있습니다. 하지만 대부분의 경우는 표준 라이브러리의 속도를 따라잡기 어렵기 때문에, 실무에서는 최대한 표준 라이브러리를 활용하는 방향으로 가는 것이 좋습니다.